We have learned about escape sequences in the previous tutorial. I hope you have practiced it well. In this tutorial, we are going to learn about Python Data Types which is the most core topic of this Python series. That is to say; it's data type or literals.
You may not have heard of the words literal and data types before if you are new to programming. But don't worry, we got you covered here! We will cover the following topics in this tutorial -
- What is Literal?
- What are Data Types?
- Integers in Python
- Floats in Python
- What is Number System in Python?
- Decimal Numbers
- Binary Numbers
- Octal Numbers
- Hexadecimal Numbers
- Key Takeaways
- Practice Yourself
What is Literal?
Literals are some data that can be identified by themselves. In other words, you can think of it as a direct value. For example, if you take a number 759, you can quickly recognize it by merely seeing it, whereas the name number can have any value in it.
That is to say, any data that can be recognized by seeing is known as a literal. Some examples of literals are 151, 7.59, 0.11, "ToolsQA," etc. We have used double-quotes for the ToolsQA example, and it is a string literal. So far, we have mentioned it as a text. From this tutorial onwards, we are going to call it with its actual name, i.e., string. Moreover, the real number 7.59, 0.11 is known as floats. Additionally, we will talk about floats later in this tutorial and strings in the next tutorial.
We have already seen how we can pass a literal in print function - print("ToolsQA").
What are Data Types?
A specific kind of data item defined by its value is known as Data Types.
As we already saw that the values are literals. Moreover, Python divided the literals into four different types of data. Data types are the building blocks for any programming language.
Python Data types are integers, floats, strings, and booleans. Additionally, they play a vital role in programming. Therefore, one should possess a strong knowledge of them. In this tutorial, we are going to learn about the integers and floats.
Python Data Type - Integer
The numbers that don't have any fractional parts are known as Integers. Additionally, it can be positive, negative, or zero. See the integers number line.
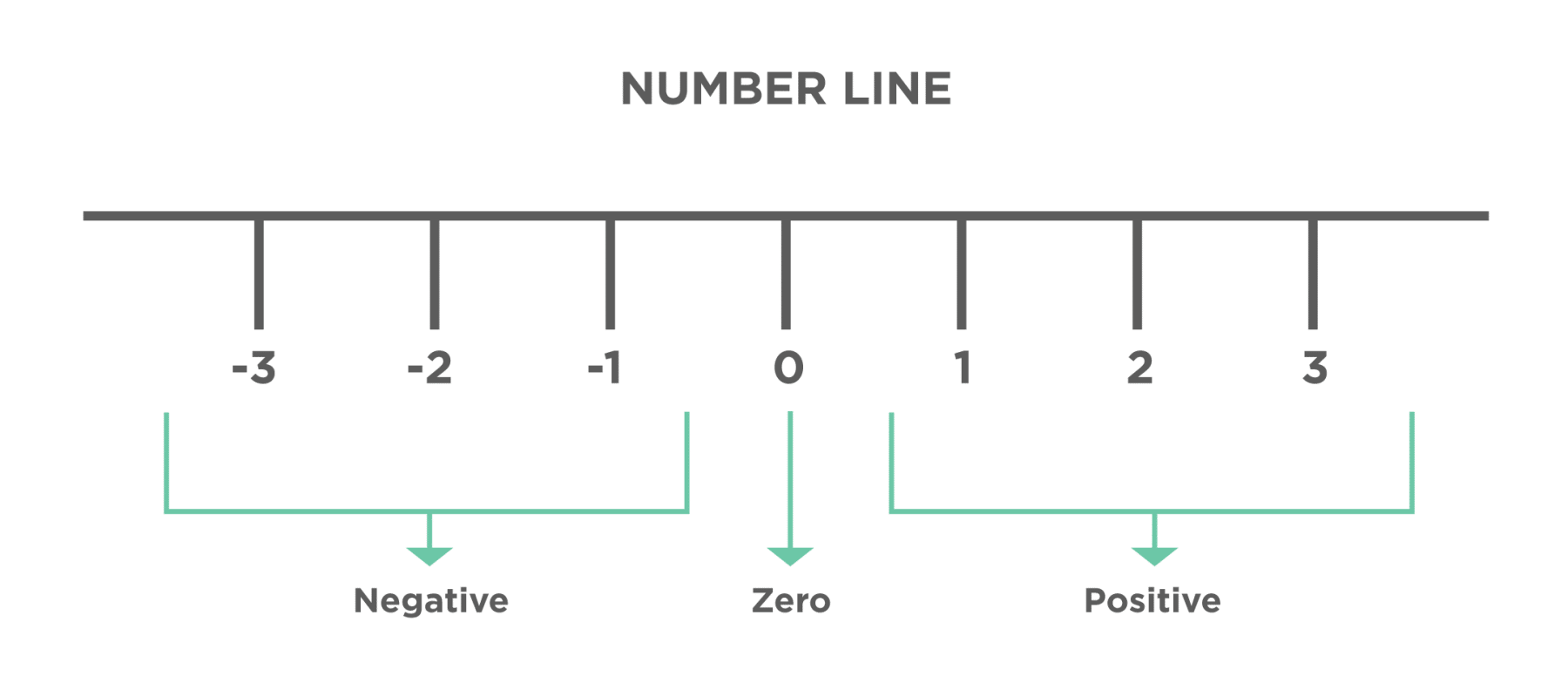
Some examples of integers are 759, -759, 123, 4, -5, etc. In addition to this, Integers don't have a fraction part. Let's see how to represent integers in Python.
We can use the integers directly as we use it generally. In other words, there is no special notation for the integers in Python. Subsequently, let's try running the following example code.
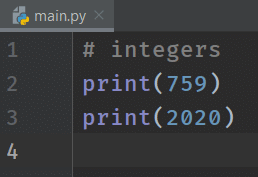
# integers
print(759)
print(2020)
The numbers that we passed to print statements are integer literals.
You will get the same output as you see in the program.

What if we want to store large numbers like 123,456,789? We can't write as it is. That is to say; Python doesn't allow us to put commas in between the digits of a number. Let's see what happens if we write them in the print statement?
# integers
print(123,456,789)
I think you know the output for the above code. Consequently, run the code and see it whether your output matches the real output or not.

We didn't get any errors. In other words, the print statement takes them as three different numbers and prints them to the console. But that's not what we want. We want the entire number as 123456789. Let's explore other ways to write long integers.
Can we write the number as 123 456 789? No, it's not correct, according to Python. So, what do we get as the output for 123 456 789? Let's check it with the following code.
# integers
print(123 456 789)
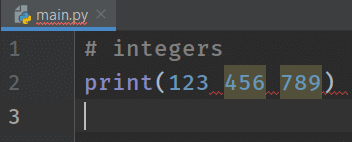
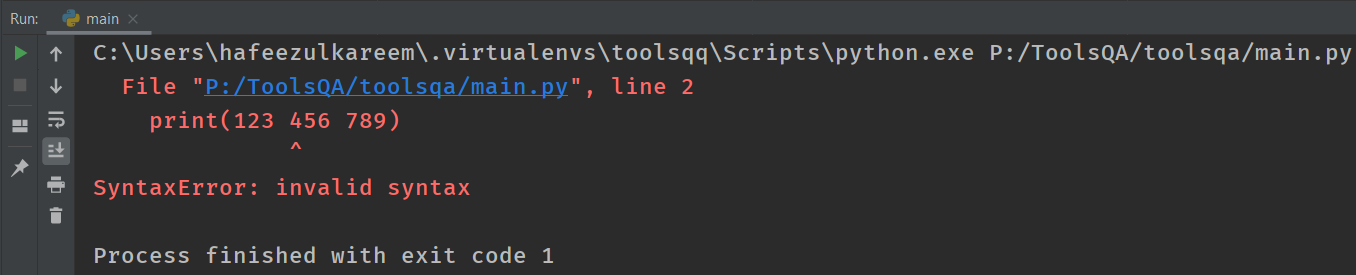
What's the correct way then?
We can write it as 123456789. We already know that it's one of the ways. But it is difficult to skim. Therefore, to avoid this, Python has a special notation for long digit integers.
Using underscore (_) in place of the comma (,) and space ( ) in the number, we can achieve the goal. As a result, the number becomes 123_456_759. The notation appears in Python 3.6 for the first time. Write the following code in the IDE and run it.
# integer with underscore
print(123_456_759)
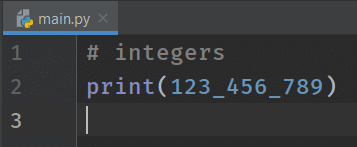

We got the correct output. In other words, it's just a notation to represent large numbers. It's your choice to use it or not. Therefore, using underscore to divide the parts of a large number is a good practice.
How to represent negative integers?
Use the hyphen (-) before the number to make it a negative number. In other words, everything else is similar to a positive number. If we don't put a hyphen (-) before a number, then Python considers it as a positive integer. Let's see the addition example with negative integers.
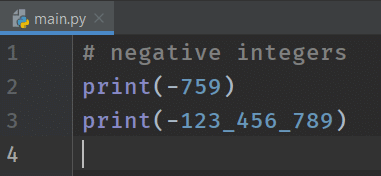
# negative integers
print(-759)
print(-123_456_789)
As shown above, we are printing the negative integers.

int() function
The function int() helps to convert a string or float into an integer. Additionally, the function int(argument) takes an optional argument. Therefore, if we don't pass anything to the int() function, then it returns a zero.
Let's see some examples of the conversion of other data types into an integer.
- If you pass a string literal that contains integer digits, then the int(string) will return the string of digits as an integer. Consequently, let's write the following code in your IDE and run it.
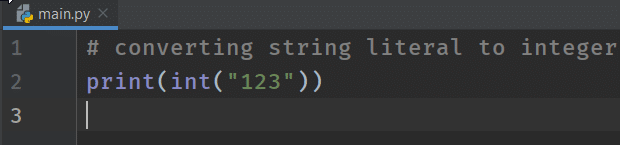
# converting string literal to integer
print(int("123"))

So how do we know that the 123 output is an integer now and not a string? Try this on your own - print (int("123") +1 ) What did you get? If you get 124, that means String "123" converts to an integer 123, and hence you can do an operation of addition on it!
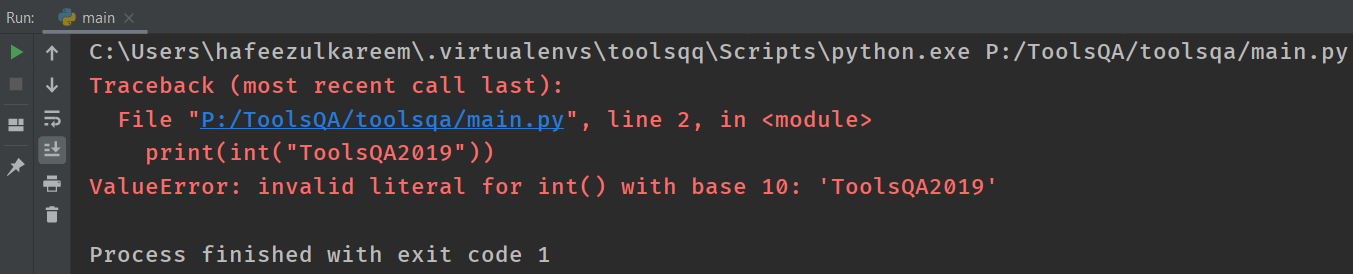
- What if you pass a text like ToolsQA2019? Can the int() convert it into an integer without any errors? Guess it. I think most of you feel that it's not possible because of the alphabets present in the string literal. And it's true. That is to say, the function int() is not able to convert the string ToolsQA2019 into an integer. It throws a ValueError.
It doesn't understand the text with characters other than digits. As a result, the function int() throws an error. See the failure by running the following code in IDE.
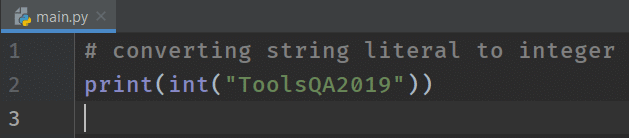
# converting string literal to integer
print(int("ToolsQA2019"))
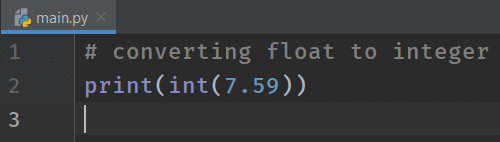
- If you pass float to the int() function, it returns the integer part of the float. In other words, say you pass the value 7.59 to the int() function. As a result, it returns the integer part, i.e., 7. Follow the below code for hands-on experience.
# converting string literal to integer
print(int(7.59))

What happens when we don't pass any parameter? Try print(int()) on your own. Consequently, you will get 0 as output.
Python Data Type - Floats
Floats contain values with fractional parts. Additionally, it has values both before and after the decimal point. Moreover, they have a unique name in programming called floating-point numbers.
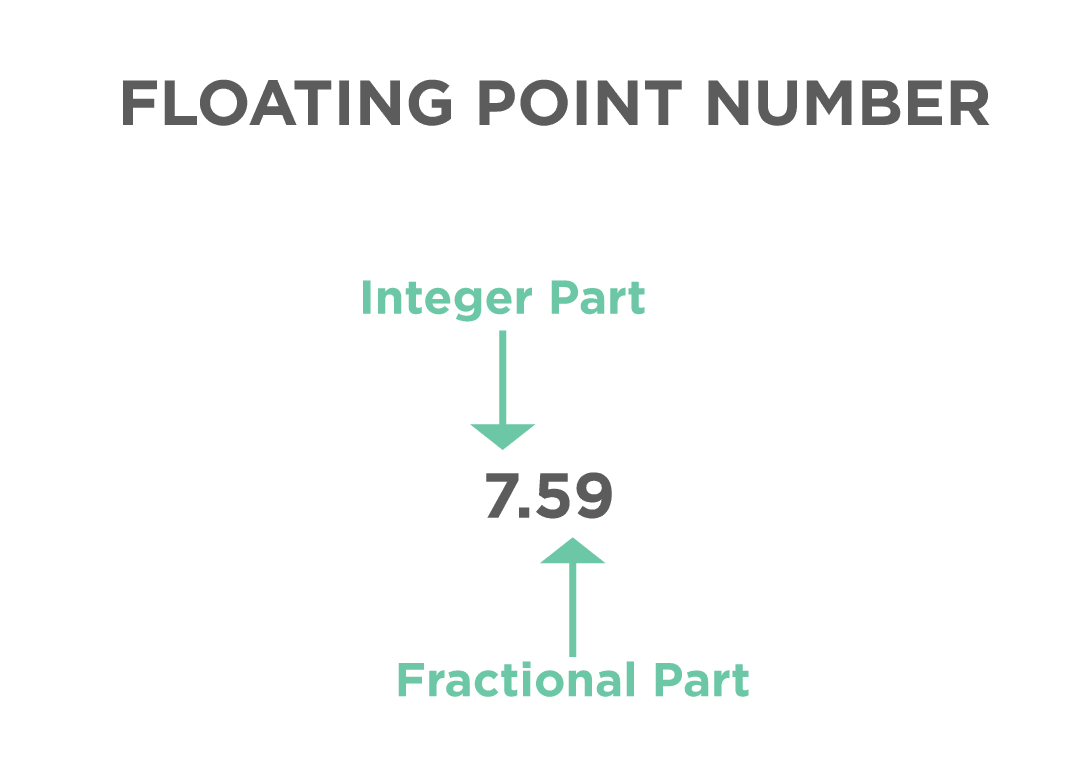
Examples of floating-point numbers are 7.59, -95.7, .7, 7., etc.
We can write the 7.0 as 7. and 0.7 as .7. In other words, we can delete the zero if it is the only digit in the integer or fractional part of the floating-point number.
Open the IDE and write the following code.
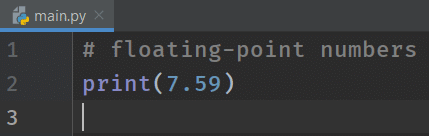
# floating-point numbers
print(7.59)
As shown above, we are printing the floating-point number.

Try to print different floating-point numbers to see the behavior of the floats in Python.
Scientific Notation
If the floating-point values are huge numbers, then we will use scientific notation to represent them. In other words, we have to use the alphabet e or E in the scientific notation.
If you see the number 7590000000000.0, it is complicated to type all the zeroes. In other words, instead of typing all the zeroes, we can represent it as 759 x 1010, which is 759E10 in scientific notation.
7590000000000.0 = 759x1010 = 759E10
In scientific notation, the part after the E must be an integer. In addition to this, before part of the E may be integer or float. Let's see some examples.
- 7.59 x 10-25 = 7.59e-25
- 0.000007 = 7 x 10-6 = 7E-6
Whenever we use E or e to represent a number, then it is a floating-point number in Python. Let's do some practice
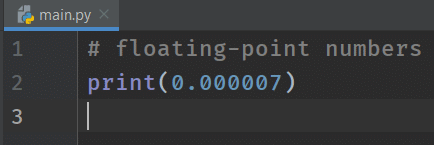
# floating-point numbers
print(0.000007)
As shown above, Python chooses the appropriate notation to display the floating-point numbers based on the value.

Therefore, Python smartly chooses to represent the output in scientific notation.
Let's see what happens if we directly print the scientific notation.
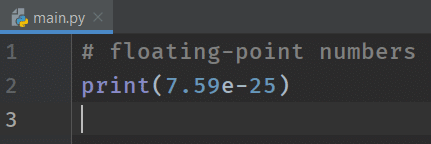

In this case, the argument was already in scientific notation, so no need for Python to make any changes.
float() function
The float() function works similar to the int() function. That is to say, it takes an object as an argument and returns the value as a float-point value. Run all the examples from the int() section using float() function. See the code examples for the conversion in the code below.
# converting to float
print(float("123.0"))
print(float(759))
print(float(7.59))
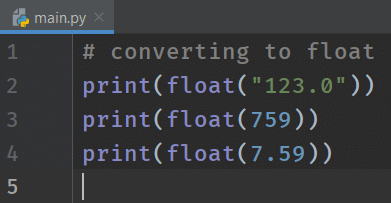

If we have given a string with characters other than digits to the float() function, it will throw an error similar to the int() function.
What is the Number system in Python?
We have different types of number systems in programming languages. Moreover, the integers that we have learned are from the decimal number system. Let's see the other number systems.
We have a total of 4 number systems. They are :
- Decimal
- Binary
- Octal
- Hexadecimal
For any number system, we will have a range of digits.
Additionally, we calculate it on the base of the number system. For example, the base of the binary number system is 2. The digits range is 0 - 1. So, in any number system, the digits range is 0 to (base - 1). Let's learn about the different number systems in detail.
Note:- print function converts any number into the decimal number system by default.
Decimal Number
We use the ***Decimal ***number system in our daily life. Moreover, they are Integers in programming. The base of decimal numbers is 10. The range of digits present in the decimal number system is 0 - 9. In addition to this, the function designed for the decimal number is int(). We have learned it in the previous section, refer to that. Let's see the expansion for a decimal number.
Take a number 16, it can be expanded as 1 * 101 + 6 * 100. Here, 10 is the base of the decimal number system. Additionally, 1, 6 are the digits of the number 16. You expand any number using the corresponding base of the number system. Let's see the remaining number of systems using the same example.
Binary Numbers
Binary means two. The base of the Binary number system is 2. So, the range of the binary number system is 0 - 1. In other words, it consists of 2 digits 0 and 1. As we all know, computers use the 1's and 0's to represent the data internally. That is to say; they use the Binary number system.
How to represent binary numbers in Python?
In Python, we will have to start a number with 0b (zero-b) or 0B (zero-B) to represent a binary number. For example, the number 2 represents 0b10 in binary notation.
We have to use a function called bin() to convert any number to a binary number. In other words, if we pass 16 to the bin() function, then it will return the binary representation of 16, i.e., 0b10000. Let's see it practically.
# decimal to binary
print(bin(16))
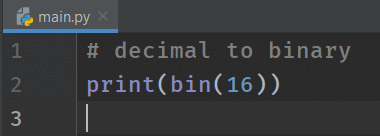

The binary representation of 16 is 10000 that can expand as 1 * 24 + 0 * 23 + 0 * 22 + 0 * 21 + 0 * 20. You can get the decimal number by computing the expansion of any number. Try it with 1111, you will get 15 as decimal number.
Octal Numbers
We have to use the prefix 0o (zero-o) or 0O (zero-O) to represent octal numbers in Python. Similar to the decimal and binary numbers, the octal number system also has the base, i.e., 8. In other words, the digits range in the octal number system is from 0 to 7. Moreover, for octal numbers, we have a function called oct(). It works similar to the int() and bin() functions. Let's see the example.
# decimal to octal
print(oct(16))
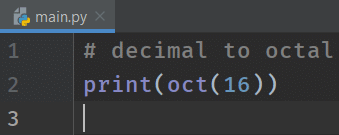

We can expand the octal number 20 as 2 * 81 + 0 * 80, which is equal to 16 in the decimal number system.
Hexadecimal Numbers
The prefix used for the representation of hexadecimal numbers in Python is 0x (zero-x) or 0X (zero-X). Moreover, the base for hexadecimal numbers is 16. So, the range of the number in the hexadecimal number system is 0 - 15. But, there is one thing that we have to learn about the hexadecimal numbers that are not in previous number systems. Let's see what it is.
One can represent the numbers in any number system using the normal digits. But in the hexadecimal number system, we have to represent the number from 10 - 15 as A - F or (a - f), respectively. See the list of numbers that has to represented using the alphabets.
| Number | Hexadecimal Representation |
|---|---|
| 10 | A or a |
| 11 | B or b |
| 12 | C or c |
| 13 | D or d |
| 14 | E or e |
| 15 | F or f |
Similar to the other number systems, hexadecimal also has a function to work with them in Python. Additionally, the function is hex(). It works similar to the int(), bin(), and oct(). Let's see the examples.
# decimal to hexadecimal
print(hex(16))
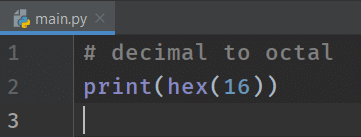
 The expansion of the hexadecimal number 10 is 1 * 161 + 0 * 160 = 16
The expansion of the hexadecimal number 10 is 1 * 161 + 0 * 160 = 16
Note:- We can pass any number system member to the functions int(), bin(), oct(), and hex(). That is to say, the number that we gave to the function will convert to the respective number system member.
Let's have a quick look at different examples. Run the following code in your IDE
# binary, octal, hexadecimal to int
print(int(0b10))
print(int(0o12))
print(int(0x19))
# int, octal, hexadecimal to binary
print(bin(2))
print(bin(0o12))
print(bin(0x19))
# int, binary, hexadecimal to octal
print(oct(12))
print(oct(0b11010))
print(oct(0x19))
# int, binary, octal to hexadecimal
print(hex(12))
print(hex(0b11010))
print(hex(0o17))
Now that we have covered so much ground let's revisit the int() function quickly again. We have seen that print(int("123")) gives 123 as output. So the int function by default converts the string to the decimal number system. However, we can also define this as int(String, base)
So if you give int("101", 2), it will take the string in binary format and give the corresponding decimal result.
print( int("101",2)) = 5
print( int("101",8)) = 65
print( int("101",16)) = 257
print( int("101",10)) = 101 (specifying base 10 is optional, so even if you write it without base, you will still get decimal base.
Till now, we have seen integers and different number systems. Now, let's see the numbers with a fractional part.
Key Takeaways
- A literal is a data that can be identified by itself. Moreover, these are fixed values. For example, 7, 7.59, "ToolsQA", 'ToolsQA', etc.
- Additionally, we can output the literals directly using the print() function.
- A particular kind of data item from the literals is known as a data type.
- There are different types of data. We have seen integer and float data types in this tutorial. That is to say, 7 is an integer, whereas 7.59 is a float data type.
- In addition to the above, there are different number systems in Python. A Binary number system has two as it's base, and it's represented by 0b - E.g., 0b1010. Similarly, the other number systems are octal, decimal, and hexadecimal. And their bases are 8, 10, and 16, respectively. Examples: 0o20, 16, and 0x10.
- *Moreover, we can use **bin(), oct(), int(), *and hex() function for the conversion of numbers from one number system to another number system.
- Small and Large numbers can be represented using scientific notation. Example: 0.000000759 => 7.59e-07 and 75900000000000000.0 => 7.59e+16.
- In addition to above, int() and float() functions convert other data types into respective data types into int and float data types.
Practice Yourself
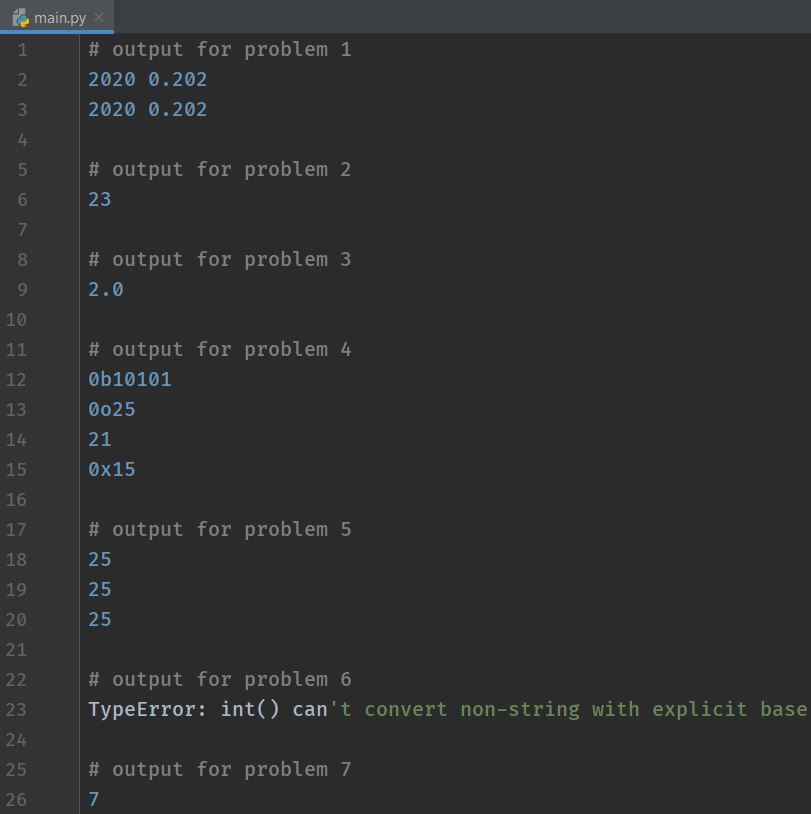
#Problem 1
print(2020, 000.202000)
print(2020, .202)
#Problem 2
print(int(23.99))
#Problem 3
print(float(2))
#Problem 4
print(bin(21))
print(oct(21))
print(int(21))
print(hex(21))
#Problem 5
print(0B11001)
print(0O31)
print(0X19)
#Problem 6
print(int(111, base=2)) # If you get an error, then try below
#Problem 7
print(int("111", base=2))
What Next?
Conclusively, that's the end of the tutorial. We have covered a lot of ground here, but the key for you is to practice all the examples.
Moreover, it was just half the fun for python literals. In our next tutorial, we will learn about boolean and String data types.
Happy Coding!