During the development of any automation framework, one of the key concepts is handling the pre and post conditions for a test case or test suite. There can be multiple situations where a specific action needs to be performed before/after either each test case or before/after all the test cases in the test suite. Following the same path, Cypress also provides the constructs which are also known as Cypress Hooks which help in performing a particular set of actions just before/after each test case or before/after all the test cases in the test suite. In this article, we will be covering the following topics to understand the Cypress tests in more detail:
- What are the constructs of a Cypress Test Script?
- What are Cypress Hooks and How to use Hooks in Cypress?
- Before() Hook
- After() Hook
- BeforeEach() Hook
- AfterEach() Hook
- Additionally, how to define hooks in a Cypress TestScript?
- How to include/exclude a Testcase from the TestSuite?
- What are Cypress Hooks and How to use Hooks in Cypress?
What are the constructs of a Cypress Test Script?
As discussed in the article "Cypress Test," Cypress uses the same constructs as provided by Mocha library to denote the concepts of TestSuite and TestCases. Let's understand some of the concepts in more detail:
How to define a TestSuite and TestCase in Cypress?
Cypress uses the "describe()" or "context()" keywords to define a test suite. Its syntax looks like below:
describe('TestSuite Name', callbackFunction {
// Specify the test cases and other steps
});
or
context('TestSuite Name', callbackFunction {
// Specify the test cases and other steps
});
E.g., we can define a sample test suite as:
describe('TestSuite1', function() {
// Specify the test cases and other steps
});
or
context('TestSuite2', function() {
// Specify the test cases and other steps
});
Where,
TestSuite1 and TestSuite2 are the names of the test suites, and we have passed an anonymous callback function as the second parameter.
Now, each test suite can one or more test cases. Cypress uses the keywords "it()" or "specify()" to define a test cases. Similar to the Test Suite, the TestCase also accepts two parameters: The first parameter is the name of the TestCase. Similarly, the second parameter is the callback function. Its syntax looks like below:
it('TestCase Name', callbackFunction {
// Test Steps
});
or
specify('TestCase Name', callbackFunction {
// Test Steps
});
E.g., we can define a sample test case as:
describe('TestSuite1', function() {
it('TestCase1', function() {
// Test Steps
});
specify('TestCase2', callbackFunction {
// Test Steps
});
});
Where,
Testcase1 and Testcase2 are the names of the test cases which exist inside the TestSuite "TestSuite1".
Now while executing the test cases or test suites, there can be multiple steps that we expect to execute before each or before all of the test cases.For example, if each test case needs the application to be in a specific state before each of the test cases or the test suite starts. In other words, it should always start from the Home page of the application. We can achieve this with the help of various "Hooks" provided by Cypress. Let's understand how these hooks can be defined and when they will invoke during the test life cycle.
What are Cypress Hooks?
As we discussed already, hooks are a way to perform a certain set of tasks before/after each/every test case. The common hooks provide by Cypress and when they will invoke can be easily understood from the following table:
| Hook | Frequency of Execution |
|---|---|
| before() | It runs once before starting the execution of first tests specified using “it” or “specify” in the “describe” or “context” block. |
| after() | It runs once after completion of all the tests specified using “it” or “specify” in the “describe” or “context” block. |
| beforeEach() | It runs before starting the execution of each of the tests specified using “it” or “specify” in the “describe” or “context” block. |
| afterEach() | It runs after finishing the execution of each of the tests specified using “it” or “specify” in the “describe” or “context” block. |
Let's understand all of these hooks in more details in the following sections:
What is a before() hook in Cypress TestScript?
As mentioned above, if you want to execute some steps only once before all the test cases, you can use the before() cypress hook to group all those test steps. It can contain some setup steps which need to perform before kicking off the test execution. Its syntax looks like below:
before(function() {
// Steps which need to be executed before all tests
});
OR
before(function namedFunction() {
// Steps which need to be executed before all tests
});
OR
before('some description', function() {
// Steps which need to be executed before all tests
});
As we can see from the above syntax, the "before block" can accept either an anonymous function, a named function, or a description and anonymous or named function.
What is an after() hook in Cypress TestScript?
As mentioned above, if you want to execute some steps only once after all the test cases have finished their execution, you can use the after() block to group all those test steps. It can contain some teardown steps which need to perform after finishing the execution of all the test cases. Its syntax looks like below:
after(function() {
// Steps which need to be executed after all tests finished execution
});
OR
after(function namedFunction() {
// Steps which need to be executed after all tests finished execution
});
OR
after('some description', function() {
// Steps which need to be executed after all tests finished execution
});
As we can see from the above syntax, the "after block" can accept either an anonymous function, a named function, or a description and anonymous or named function.
What is a beforeEach() hook in Cypress TestScript?
As mentioned above, if you want to execute some steps before each of the test cases in the TestSuite, you can use the beforeEach() block to group all those test steps. It can contain some setup steps which need to perform before kicking off the test execution of each of the test case. It can be something like bringing the application to a specific state before each test case. Its syntax looks like below:
beforeEach(function() {
// Steps which need to be executed before each test case
});
OR
beforeEach(function namedFunction() {
// Steps which need to be executed before each test case
});
OR
beforeEach('some description', function() {
// Steps which need to be executed before each test case
});
As we can see from the above syntax, the "beforeEach block" can take either an anonymous function, a named function, or a description and anonymous or named function.
What is an afterEach() hook in Cypress TestScript?
As mentioned above, if you want to execute some steps after each of the test cases in the TestSuite has finished their execution, you can use the afterEach() block to group all those test steps. It can contain some teardown steps which need to perform after finishing the execution of each of the test cases. It can be something like bringing the application or database to a specific state after each test case. Its syntax looks like below:
afterEach(function() {
// Steps which need to be executed after each of the tests which finished execution
});
OR
afterEach(function namedFunction() {
// Steps which need to be executed after each of the tests which finished execution
});
OR
afterEach('some description', function() {
// Steps which need to be executed after each of the tests which finished execution
});
As we can see from the above syntax, the "afterEach block" can accept either an anonymous function, a named function, or a description and anonymous or named function.
Let's understand the execution order of all these hooks, with the help of following code snippet:
// type definitions for Cypress object "cy"
/// <reference types="cypress" />
describe('Cypress Test Hooks', function() {
before(function() {
// runs once before all tests in the it block
cy.log("I am in before")
})
after(function() {
// runs once after all tests in the it block
cy.log("I am in after")
})
beforeEach(function() {
// runs before each test in the it block
cy.log("I am in beforeEach")
})
afterEach(function() {
// runs after each test in the it block
cy.log("I am in afterEach")
})
it('Cypress Test Case 1', function() {
// Test Steps/Commands for Test Case 1
cy.log("I am in Test Case 1 ")
})
specify('Cypress Test Case 2', function() {
// Test Steps/Commands for Test Case 2
cy.log("I am in Test Case 2")
})
})
Save the above code in file "cypressTest1.js" under the integration/example folder and run Cypress using the command "./node_modules/cypress/bin/cypress open". It will open the Cypress dashboard. Now run the test case by double-clicking on the "cypressTest1.js" file. It will show the sample output as follows:
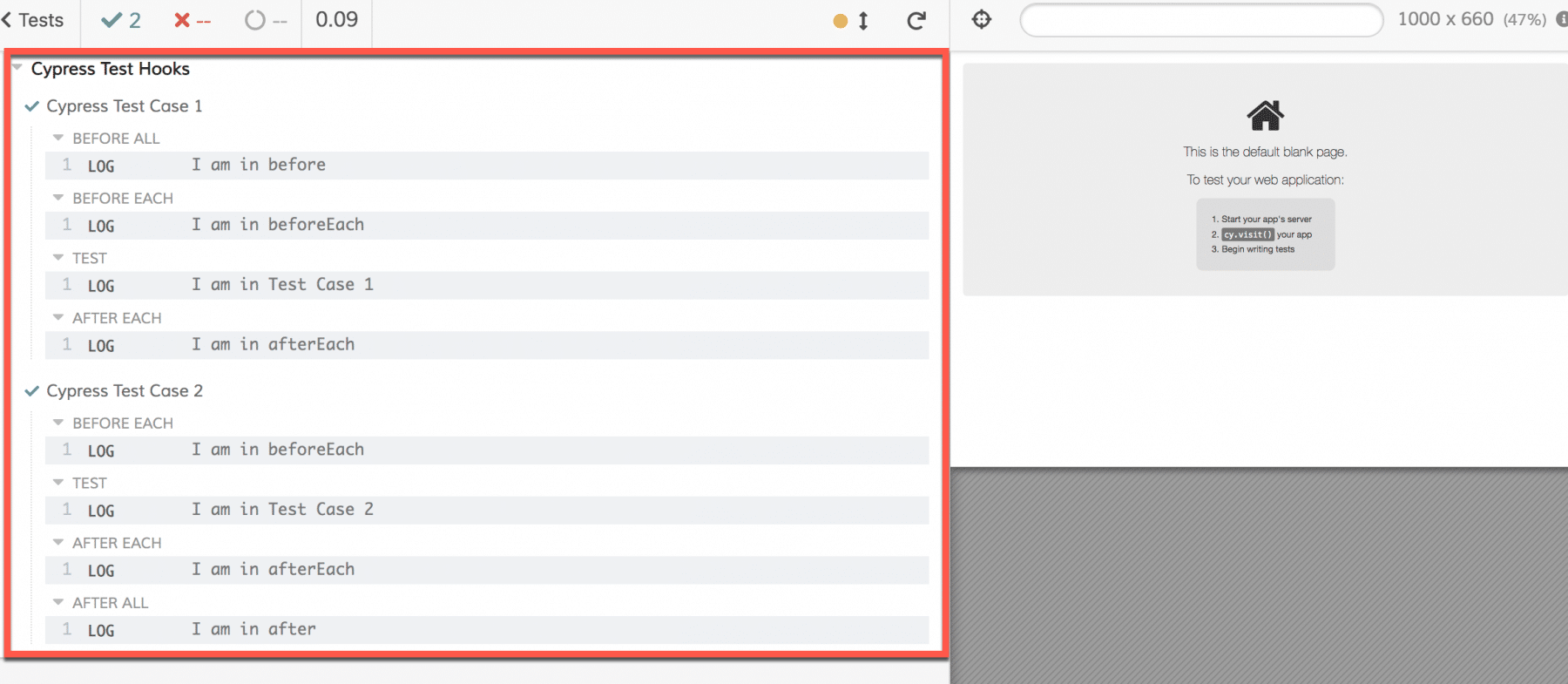
- As we can see from the above test execution screenshot that the first step executed as a part of Cypress Test Case 1 is 'BEFORE AL.' Moreover, it ran the steps mentioned under the "before()" block.
- Further, we can see that the last step of Test Case 2 is 'AFTER ALL.' Additionally, it executed the steps mentioned under the "after()" block.
- Also, we can see that the 'BEFORE EACH' step executed before executing every test case. Also, it is present in each Cypress Test Case. It executes the steps mentioned under the "beforeEach()" block.
- 'AFTER EACH' step is executed after every test case and is present in each Cypress Test Case. It executes the steps mentioned under the "afterEach()" block.
- Apart from these, we can see the tests specified using the "it" and "specify" blocks that execute in the order as mentioned in the file.
Now, there can be scenarios when we want to execute only a specific test case from the TestSuite. In addition to this, we also want to skip a particular test case from the TestSuite. Let's understand in the following section that we can achieve the same using few of the constructs provided by Cypress:
How to include/exclude a Testcase from the TestSuite?
When we have a list of test cases or test suites in a Cypress TestScript. Moreover, we need some flexibility to run only a few of them on a need basis. If the list of test cases /test suites which need to execute is smaller, then we can use the inclusion strategy. Its purpose is to include only the specified test cases or test suites in the planned test run. But, on the contrary, if the list of test cases or test suites to be executed is much bigger compared to the list of the test-cases/test-suites which need to skip from the test run, then we can opt for the exclusion strategy.
Cypress provides two tags: ".only" and ".skip"to implement the inclusion/exclusion strategy for the test runs. If you want to execute only specific test cases in a test suite or want to execute a particular test suite in the test script, you can append those with the ".only" tag. Its syntax looks like below:
// Including a Test Suite
describe.only('TestSuite1', function() {
})
or
context.only('TestSuite2', function() {
})
// Including a Test Case
it.only('Test Case 1', function() {
})
or
specify.only('Test Case 2', function() {
})
Let's understand the usage of ".only" tag with the help of following code snippet:
// type definitions for Cypress object "cy"
/// <reference types="cypress" />
describe('Cypress Test Hooks', function() {
it('Cypress Test Case 1', function() {
// Test Steps/Commands for Test Case 1
cy.log("I am in Test Case 1 ")
})
specify('Cypress Test Case 2', function() {
// Test Steps/Commands for Test Case 2
cy.log("I am in Test Case 2")
})
it.only('Cypress Test Case - 3', function () {
// Test Steps for Test Case - 3
cy.log("I am only in Test Case 3") })
})
Run the above test case by saving the same in a test file say "cypressTest2.js". It will show the sample output, as shown below:
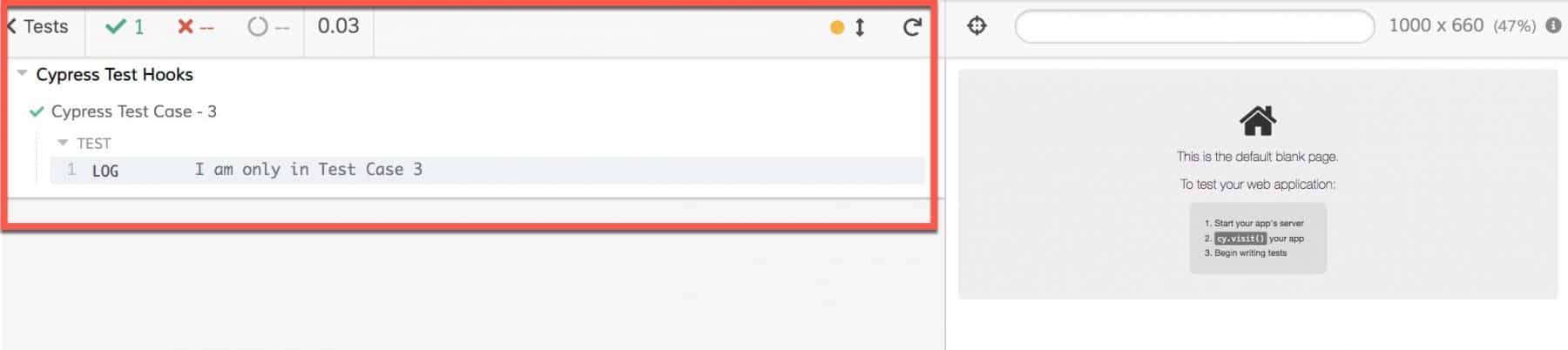
As we can see, even though there were three test cases in the test suite. However, the Cypress only executed the "Cypress Test Case - 3", because of its explicit ".only()" tag. Whenever any TestSuite contains one or more than one test, which is tagged with the ".only" tag, then Cypress will execute only those test cases. Moreover, it will skip the remaining from the test run.
On the other hand, if you want to skip a particular test case or test suite, you can use the ".skip" tag. Its syntax looks like below:
// Excluding a Test Suite
describe.skip('TestSuite1', function() {
})
or
context.skip('TestSuite2', function() {
})
// Excluding a Test Case
it.skip('Test Case 1', function() {
})
or
specify.skip('Test Case 2', function() {
})
Let's understand the usage of ".skip" tag with the help of following code snippet:
// type definitions for Cypress object "cy"
/// <reference types="cypress" />
describe('Cypress Test Hooks', function() {
it('Cypress Test Case 1', function() {
// Test Steps/Commands for Test Case 1
cy.log("I am in Test Case 1 ")
})
specify('Cypress Test Case 2', function() {
// Test Steps/Commands for Test Case 2
cy.log("I am in Test Case 2")
})
it('Cypress Test Case - 3', function () {
// Test Steps for Test Case - 3
cy.log("I am only in Test Case 3") })
it.skip('Cypress Test Case - 4', function () {
// Test Steps for Test Case - 3
cy.log("I am in skip Test Case 4") })
})
Run the above test case by saving the same in a test file say "cypressTest3.js". It will show the sample output, as shown below:
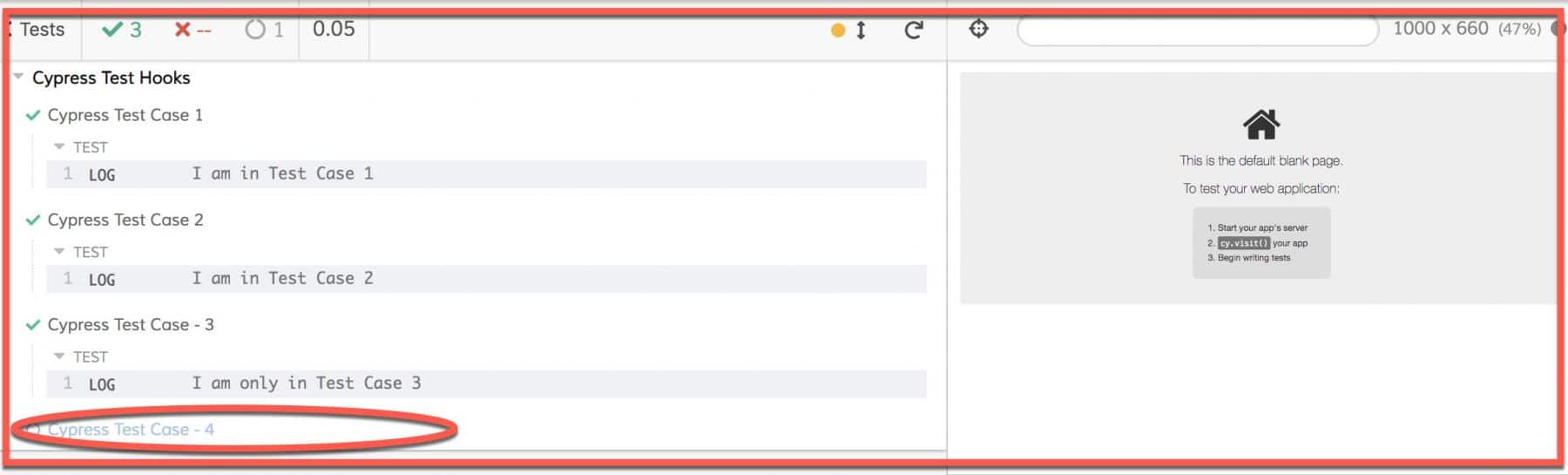
Here in the above screenshot, we can see that Cypress Test Case 4 was not executed. Instead, it was skipped, and the other 3 test cases were executed.
Key Takeaways
- Cypress provides describe and context keywords to define a test suite.
- Cypress provides it and specifies keywords to define a test case.
- Moreover, Cypress provides various hooks like before, beforeEach, after, and afterEach to execute certain pre and post steps.
- Cypress provides only and skip tags to include/exclude specified test case/test suites from a specified test run.
Let's move to the next tutorial, where we will learn about Fixtures. Additionally, we will also understand how it is an important aspect of the Automation Framework for Cypress.
If you want to learn more you can look at this video series: ++Cypress video series++