We already know that Black box testing involves validating the system without knowing its internal design. Testing a black-box wFay is a more natural way to test. However, it brings its complexity that the number of test conditions can have several hundred variations. So how do we keep the total number of test cases to a minimum and yet ensure that we have good test coverage? Few black-box techniques have evolved to address this complexity, which is time tested and scientific. We will discuss one such test case design technique known as Equivalence Partitioning.

• What is Equivalence Partitioning?
• How to do Equivalence Partitioning?
• What are its Pitfalls?

What is Equivalence Partitioning?

Equivalence partitioning is a black-box testing technique that applies to all levels of testing. Most of us who don't know this still use it informally without even realizing it. But there are defined rules and best practices that can make it more useful and scientific.

The idea behind the technique is to divide a set of test conditions into groups or sets that can be considered as same. Partitioning usually happens for test objects, which includes inputs, outputs, internal values, time-related values, and for interface parameters. Equivalence Partitioning is also known as Equivalence Class Partitioning.  It works on certain assumptions:

• The system will handle all the test input variations within a partition in the same way.
• If one of the input condition passes, then all other input conditions within the partition will pass as well.
• If one of the input conditions fails, then all other input conditions within the partition will fail as well.

The success and effectiveness of Equivalence partitioning lie in how reasonable the above assumptions hold. We will discuss this in detail in the latter part of the article with practical examples where these assumptions hold or fail.

How to do Equivalence Partitioning?

Now that we have a fair idea of equivalence partitioning, let's discuss how to do partitioning effectively.

Consider that you are filling an online application form for a gym membership. What are the most important criteria for getting a membership? Of course, the age! Most of the gyms have age criteria of 16-60, where you can independently get the membership without any supervision needed. If you look at below membership form, you will need to fill age first. After that, depending on whether you are between 16-60, you can go further. Otherwise, you will get a message that you cannot get a membership.

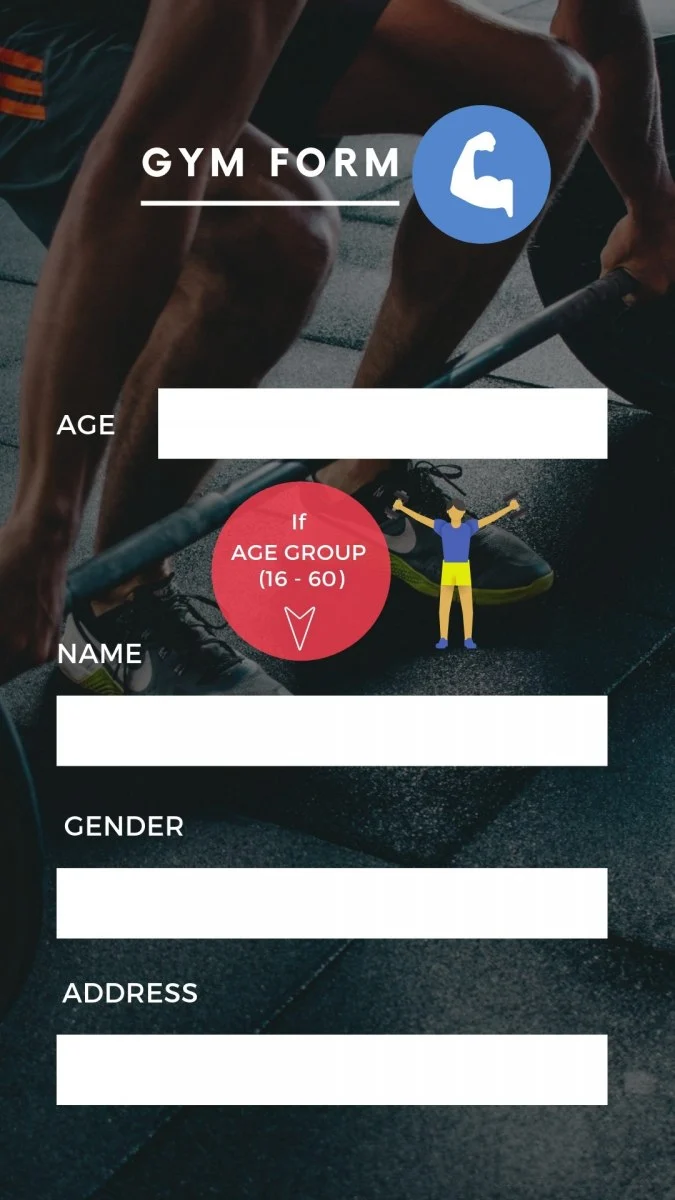
If we have to test this age field, the common sense tells us that we need to test the values between 16-60, and values which are less than 16, and some values which are more than 60. It is easy to figure out, but what is not very evident is how many combinations we need to test to say that the functionality works safely?

• <16 has 15 combinations from 0-15, and if you test negative values, then some more combination can be added
• 16-60 has 45 combinations
• >60 has 40 combinations (if you only take till 100)

Should we test all these 100+ combinations? Surely! If we had all the time in the world, and the cost was not an issue at all. Practically we can never do that because there is minimal time for testing.

Additionally, we need to ensure that we create minimal test cases with maximum test coverage. It is where the testing techniques come into the picture. Let's see how Equivalence Partitioning will solve this problem.

The First step in Equivalence partitioning is to divide (partition) the input values into sets of valid and invalid partitions. Continuing the same example our partition will look like below -

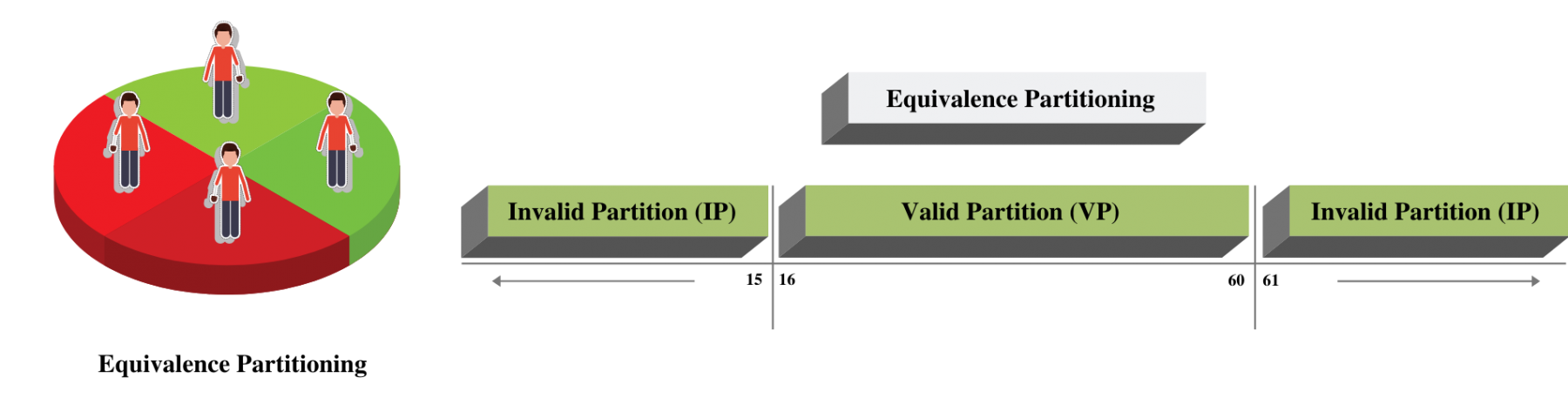
Valid Partitions are values that should be accepted by the component or system under test. This partition is called "Valid Equivalence Partition."

Invalid Partitions are values that should be rejected by the component or system under test. This partition is called "Invalid Equivalence Partition."

So what should we do after knowing these partitions? The premise of this technique works on the assumption that all values within the partition will behave the same way. So all values from 16-60 will behave the same way. The same goes for any value less than 16 and values greater than 60. As such, we only test 1 condition within each partition and assume that if it works/doesn't work, the rest of the condition will behave the same way.

Our Test conditions in Such case could be:

• Enter Age = 5
• Enter Age = 20
• Enter Age = 65

If you see, these 3 test conditions will cover the 100+ conditions that were not possible otherwise. By applying this technique, we have significantly reduced our test cases, but yet the coverage remains high.

These partitions can be further divided into sub-partitions if required - Let's understand it by expanding the same example of Gym membership. Let's assume that if you are 16-20 years old or 55-60 years old, there is an additional requirement to attach your age proof while submitting the membership form. In this case, our partition will look like below-

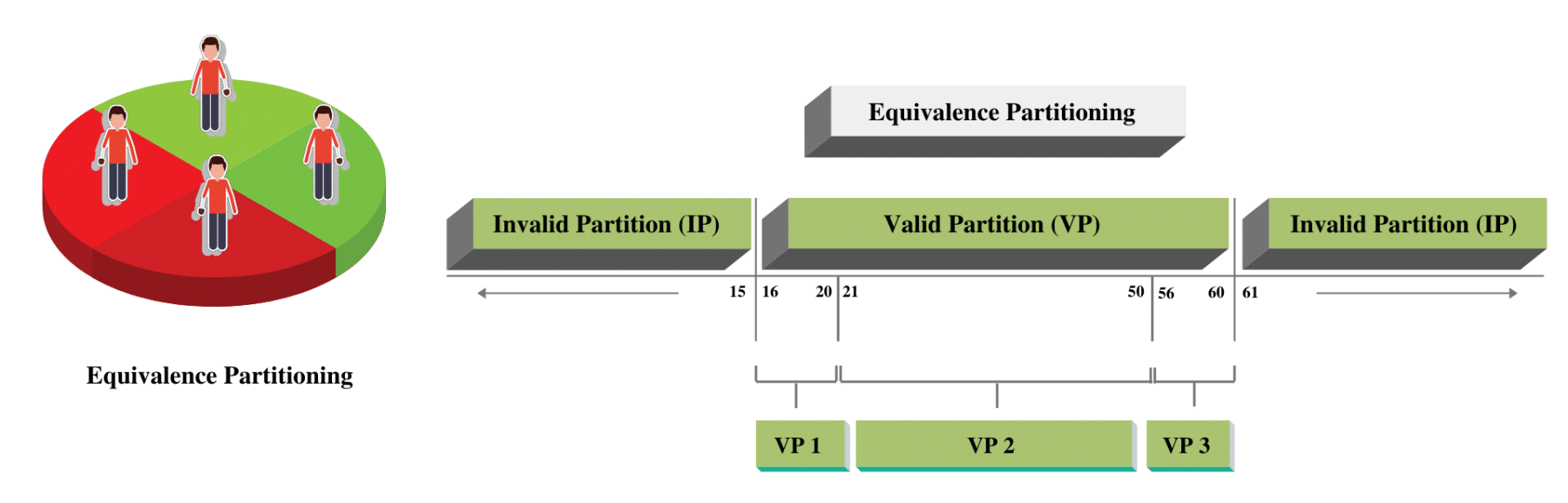
VP1, VP2, and VP3 are all valid subpartitions based on the additional requirements. So how do our test conditions look like now?

• Enter Age = 5
• Enter Age = 18
• Enter Age = 30
• Enter Age = 58
• Enter Age = 65

These five conditions will cover all the requirements that we have for the age field. Of course, you can use any other values from each partition as you like.

We need to ensure that our partitioning is unique and not overlapping. Each value that you take should belong to only one partition.

When we use invalid equivalence partitions, their testing should happen individually and not combined with other partitions or negative inputs. E.g., if you have a name field which accepts 5-15 characters (a-z). If you try to enter abc@, this gives an error, but we don't know whether the error is because we have entered four characters, or it's because we have used "@". Thus combining two invalid partitions or negative values, we end up masking the actual root cause.

To achieve 100% coverage, we should ensure that our test case covers all the identified partitions. We can measure the Equivalence partitioning test coverage as the number of partitions tested by at-least one value divided by the total number of recognized partitions.

Pitfalls

Now that we know how useful equivalence partitioning is, let's try to understand some of its pitfalls.

The success of Equivalence partitioning is dependent on our ability to create correct partitions. Sounds simple right? If you dig deeper, you will realize that we are testing the application as a black box. Therefore, our ability to create partition limits to what is called out in requirements. We have no understanding of designs and what the developer would have coded.

If we take our Gym example - Let's assume developer wrote below logic-

If (age > 16 and Age <60 )

{ Allow the user to submit the form}

Do you see the problem here? The requirement said age should be greater than or equal to 16. If we go by partition rule, we might miss checking 16 as value. Also, the partition doesn't cater to other negative values like entering non-numeric characters (@, abc, etc.). So while partitioning helps us minimize our test cases to maximize coverage, we need to be aware that it doesn't cover all the combinations required to test the application successfully.

It concludes our discussion on Equivalence partitioning.

Discussions on using techniques like Boundary Value Analysis to cover up some of the pitfalls of using partitioning alone will be taken up in the subsequent articles.