I was born on January 26, 1993.. Yawn. Mind starts day-dreaming. Goes to the kitchen and grab something to eat. Sit back down at the computer. My mother’s name is Wonder Woman a.k.a…. Wait, I haven’t seen the new Marvel movie trailer yet. Hits Youtube. Return to the word processor. My mom has two children…
Suddenly, I realize it will take forever to write about my jumbo family. And who would want to read the wall of text, anyway? Shutdowns processor. Starts Netflixing.
Ever had this problem of introducing all members of your family to the newest friend? Me, too. And I have like 15 members to introduce so I hope you understand why it was so overwhelming for me to write about them.
So, I did best I could think of. I drew a diagram. A family tree to be precise.
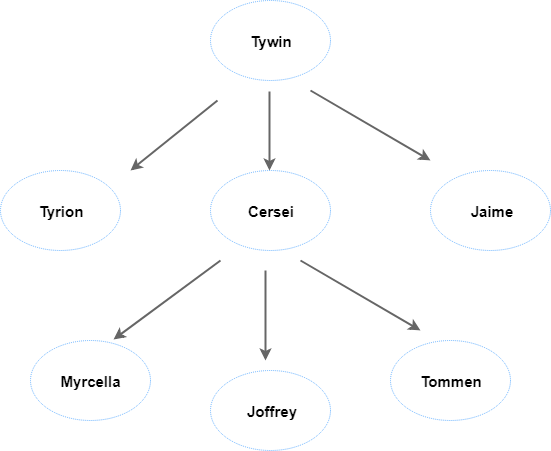 Okay...This isn't my family. This diagram is based on the famous TV show Game of Thrones. But, hey, it saved me from writing this huge wall of words. This family tree accurately shows us the hierarchy of House Lannister.
Okay...This isn't my family. This diagram is based on the famous TV show Game of Thrones. But, hey, it saved me from writing this huge wall of words. This family tree accurately shows us the hierarchy of House Lannister.
Linear Vs Non-Linear Data structures:
A wise woman once said, Think non-linearly. Out of the box is so mainstream. So far, we’ve dealt with the data structure which were something called as linear structures. Linear data structures like an array, linked lists, stacks or queues are order dependent.
The above data structures can only be traversed sequentially. But, we've something called as non-linear data structures like trees where stored data doesn't really follow an order.
So, in absence of any order, we can traverse these structures in a non-sequential manner. Trees are known to organize their data hierarchically.
Example of hierarchy was the above family tree example.
Trees Terminology:
Let’s take an example of Document Object Model (DOM) a.k.a HTML document structure. (If you are still unfamiliar with what I am talking about, just open the F-12 developer tool and see the HTML structure. You can even open this pages source code).
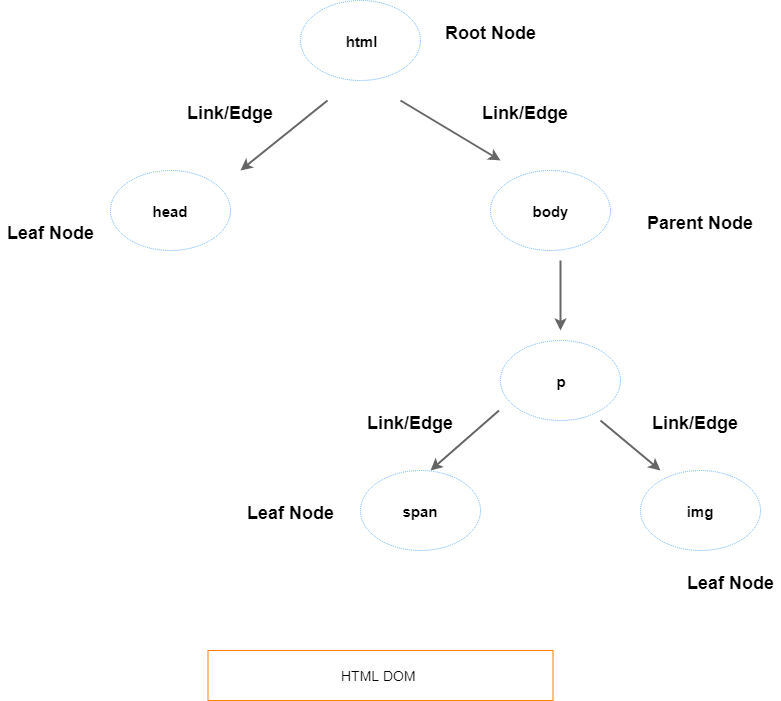 Mentioned below are some trees terminology commonly used. Just like our trees in nature; it has roots, branches, and leaves. But, with only one difference, that tree here has root at the top.
Mentioned below are some trees terminology commonly used. Just like our trees in nature; it has roots, branches, and leaves. But, with only one difference, that tree here has root at the top.
- Nodes: Like, we can see, DOM has many tags like
<html>,<head>,<body>. Let’s nickname them nodes. - Root: The topmost
<html>tag(read:node) is nicknamed as root. There is always one root to every tree. - Link/Edge: Now, this mighty root has two nodes connected to it. This connection is biological. Meaning
<html>tag(Read:Root) is the parent of<head>and<body>tag. And this biological link between them is known as edges. - Parent: Any node that has a link to another node. As discussed above,
<html>tag is the parent of<head>and<body>tag. - Sibling: Someone who has the same parents are the sibling to each other. Example,
<head>and<body>tag are siblings. - Leaf: Any node that doesn't have a child node in the tree.
Powered by our old tree vocabulary with updated versions, let’s talk about a very famous tree structure.
Binary Tree:
A binary tree can be simply defined as a tree structure with a maximum of two child nodes from any other node.
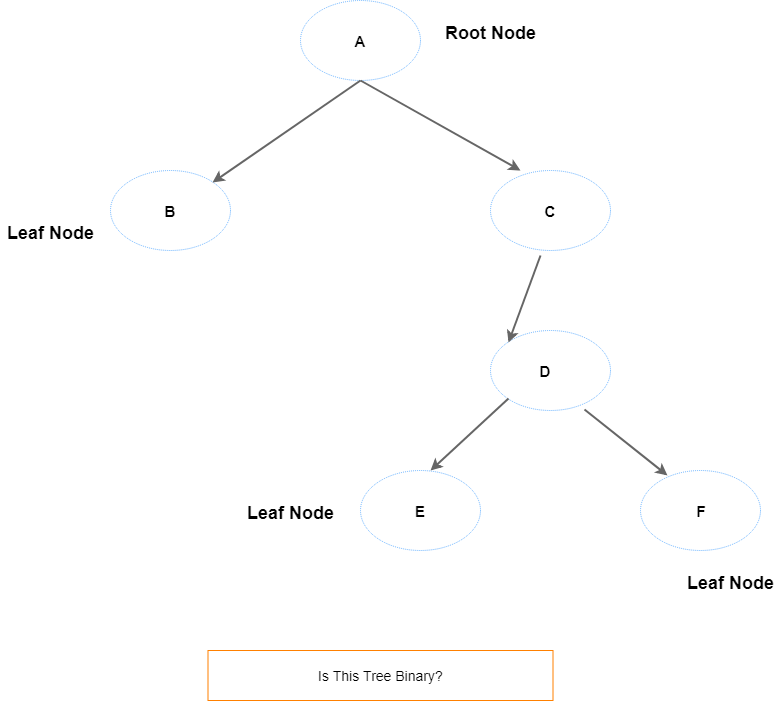 Is this above tree binary?
Is this above tree binary?
Let me walk through the above definition. And also, tell you how to identify the binary tree.
Now, to decide whether the tree given to us is binary or not, we simply need to remember one golden rule:
Any node present in the tree can have a maximum of two child nodes from other nodes. When we say maximum two, it means the node can have no child node(this is our root node). Or it could have one node. Or two.
But, never more than two.
Back to our tree, root node A has two children. Node B has no child node. Node C has one child. Node D has two children.
All points check. It is a binary tree.
What Is So Special about Binary Tree?
Because Binary trees are often used for implementing a wonderfully searchable structure called, not surprisingly, a binary search tree or BST.
Binary Search Tree (BST):
(Also, fondly known as Ordered Tree or Sorted tree)
The Binary Search tree is just like Binary Tree with some modifications to support fast search.
Binary Search tree follows two golden rules here:
- Each node cannot have more than two intermediate children (binary tree rule)
- Left child of the node must be less than the parent and a right child must be more than a parent.
Let’s start constructing a binary search tree through an example.
Remember, the associative array we studied during hash tables? Binary Search is often used to sort key-value pair in the associative array.
arr = {
50 : ‘a’,
25 : ‘b’,
100 :’c’
75: ‘d,
}
Let’s add keys one by one :
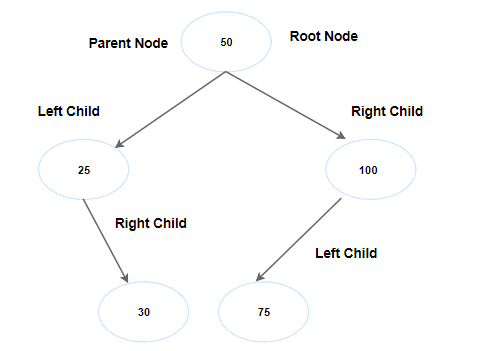
The first key is 50, so this becomes our root node.
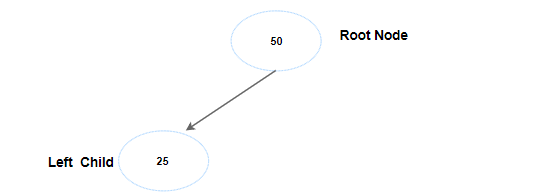
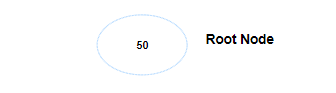 Next key is 25, Binary Search Tree evaluates it and says, “Ah, this is less than parent node 50, so this will be left child".
Next key is 25, Binary Search Tree evaluates it and says, “Ah, this is less than parent node 50, so this will be left child".
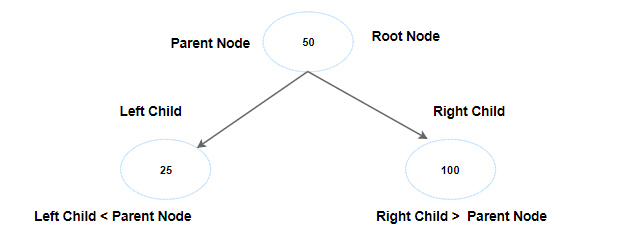
 Now, the next key is 100, BST evaluates it and says, “This is greater than a parent node 50, so this will be the right child”
Now, the next key is 100, BST evaluates it and says, “This is greater than a parent node 50, so this will be the right child”
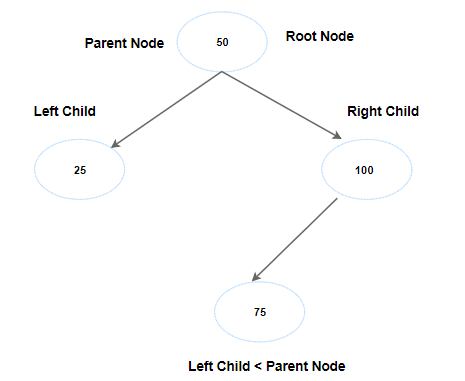
 Now does the golden rule no 2 of BST makes sense?
Now does the golden rule no 2 of BST makes sense?
Next key is 75, BST evaluates it and says, “This is greater than a parent node 50, so this will be the right child”
But, “uh-oh! We have a problem. 100 already is sitting as for right child”
No problem. Let’s compare 100 with 75. Since 75 is less, it becomes left child of 100.
 Next key is 30, BST evaluates it and says, “This is less than a parent node 50, so this will be a left child”
Next key is 30, BST evaluates it and says, “This is less than a parent node 50, so this will be a left child”
We have the same problem again. 25 sits as the left child. So, we compare 30 with 25. As 30 is greater than 25, it becomes the right child.
 But, hey, we don’t just use data structures for storing of data. We need to perform other operations like search or finding data from data structures.
But, hey, we don’t just use data structures for storing of data. We need to perform other operations like search or finding data from data structures.
How to Retrieve Or Search for Data in BST?
Let’s say we’ve to find key 75 from our above tree. We simply follow our golden rule no 2. Remember anything less than parent node becomes the left child or if greater, becomes the right child.
- Compare 75 with the root node.
- The value is greater than the root node, This key has to be somewhere on the right-hand side of the tree. Time to explore right sub-tree.
- The right child value is greater than the 75. So, time to search left subtree of node 100. And there lies our 75
The key point here is each time we’re heading down, we discard entire sections of the tree so it’s a very quick way to find a specific element.
Unbalanced Tree:
Now, you've probably noticed that we have more levels of nodes on the right hand side than on the left.
Now, it's not unusual for this kind of thing to happen. We can't always guarantee that the way data is added will allow us to build a tree with a perfectly symmetrical structure all the way down. In this case we say that our tree is unbalanced. There are more levels on one side than on the other. The downside of this is it means, on average, we would have to perform more checks to find or insert or delete any values on the right hand side than we would on the left.
Using Heap Data Structures:
Now, before I discuss the nitty-gritty of this structure, I want to put across this point: the term heap here doesn't deal with the area of memory where objects are allocated. A Heap is a data structure which has many useful purposes. It is often used in a sorting algorithm known as heap sort. Along with this, they are also a way of implementing abstract data types(ADT) like the priority queue which we discussed earlier in the series.
Now, you may be wondering, we were discussing binary trees, how did we land here.
So, let me tell you this: Heaps are usually implemented as a binary tree(please note not as a binary search tree). Now, heap just like our tree will be used to store a collection of data and we would add items top to bottom, left to right.
So, let's recall our golden rule of the binary tree - a collection of maximum two nodes under a parent. But, we use this golden rule in heaps with one simple twist.
The only twist which makes heaps different is we do not add things in random order here. Before constructing a heap, we always have to answer one question: Do we want our heap to be a min heap or a max heap?
Min Heap Or Max Heap?
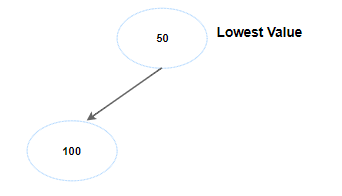
In simple words, if we want our heap to be a min heap, we would want the root node(topmost node) to store the lowest value of a collection of data.
Min-heap rule: a child nodes must always be greater than its parent.
Can you guess what max heap rule will be?
If we want our heap to be a max heap, we would want the root node(topmost node) to store the highest value of a collection of data.
Max-heap rule: a child nodes must always be less than its parent.
Let's see a Min-Heap in action.
Min Heap Example:
arr = {
50 : ‘a’,
100 :’c’
75: ‘d,
99: ‘e’,
47: 'f
}
Let's add this keys one by one.
The first key is 50, which becomes our root node.
 The next key is 100. In heaps, we add nodes, top to bottom, left to right. And, remember our topmost root node should store the lowest value of the key. Now, 100 is more than 50, it becomes the left child.
The next key is 100. In heaps, we add nodes, top to bottom, left to right. And, remember our topmost root node should store the lowest value of the key. Now, 100 is more than 50, it becomes the left child.
 Next key is 75, this is less than the root node and right child is empty, so let's place it there.
Next key is 75, this is less than the root node and right child is empty, so let's place it there.
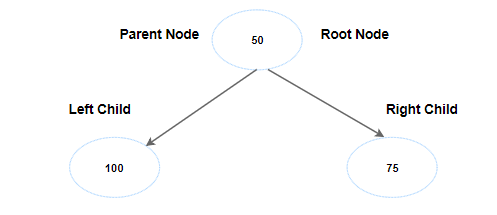 If you observe carefully, we really don't care that left child is more than its sibling. That rule was applicable in BST. Since its a min heap, the only thing we care about is parent node value should be less than its children and it should have a maximum of two nodes(binary tree rule)
If you observe carefully, we really don't care that left child is more than its sibling. That rule was applicable in BST. Since its a min heap, the only thing we care about is parent node value should be less than its children and it should have a maximum of two nodes(binary tree rule)
Next key is 99, both slots are full of the root node, so we place 99 as the left child of node 100.
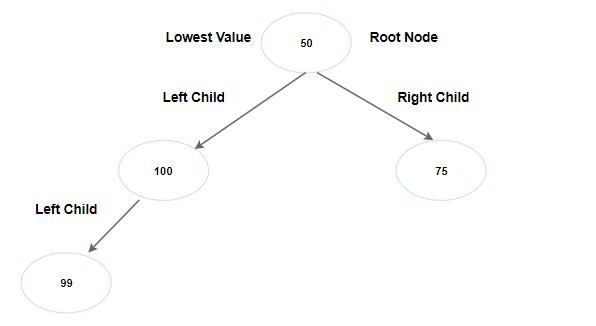 But, we run into one problem. parent node 100 is greater than 99. We are building min heap, parent node should be less than the child node. Swap 100 with 99. Now, let's check is 99 less than its parent node. No. We can proceed.
But, we run into one problem. parent node 100 is greater than 99. We are building min heap, parent node should be less than the child node. Swap 100 with 99. Now, let's check is 99 less than its parent node. No. We can proceed.
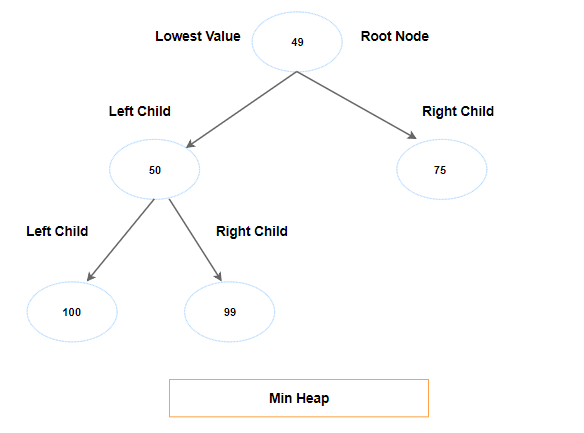
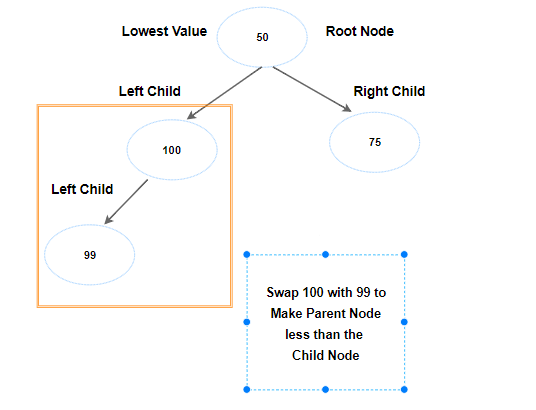 Next key is 49. Let's make it as the right child of node 99. Again, we run into min heap issue. No problem, let's swap 49 with 99.
Next key is 49. Let's make it as the right child of node 99. Again, we run into min heap issue. No problem, let's swap 49 with 99.
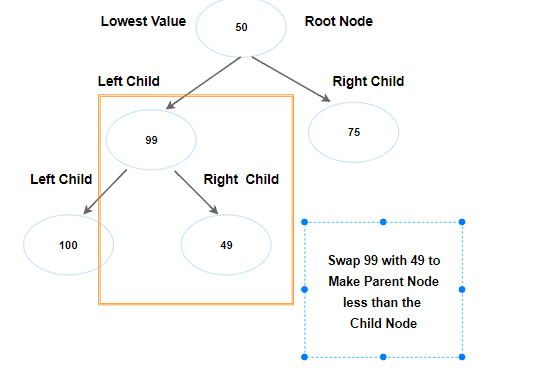 Before proceeding further, let's check if 49 is less than its parent node. Yes, it is. Let's swap that too.
Before proceeding further, let's check if 49 is less than its parent node. Yes, it is. Let's swap that too.
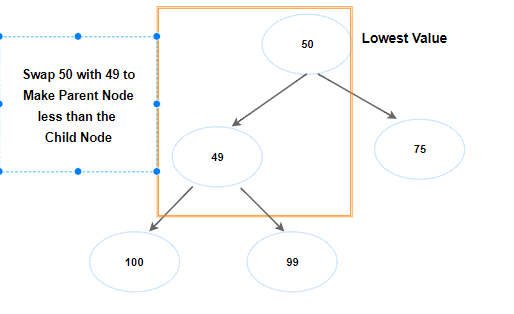 In this way, in min heap, we always bubble up to the lowest value in the collection as the root node.
In this way, in min heap, we always bubble up to the lowest value in the collection as the root node.
 The max heap is completely opposite. Here, we bubble up to the highest value of the collection to the root node.
The max heap is completely opposite. Here, we bubble up to the highest value of the collection to the root node.
Priority queues:
Heap is not a fully sorted data structure. The one thing we can be sure about is that the minimum or the maximum value will always be at the top.
Just because of this one thing, heaps are most useful for the idea of priority queues. Here, we didn't care about the order much. If we want some object to be given priority and pushed ahead in the queue, we could give it a low number and see it bubble to the top.
Heap - Language Support
| Language | Support |
|---|---|
| Java | Priority Queue |
| C# | N/a |
| Python | heapq |
| Ruby | N/a |
| C++ | std::priority_queue |