I have got a baby niece. She completed a total of three years on this planet. To celebrate her existence, I decided to teach her about linked list. I decided to buy her four gifts (I am a generous aunt)
Now, I could’ve given her the gifts directly but I want to trouble her a little (C’mon, don’t get all judgy now. She has kept me up so many nights with her shrieks. Time to trouble her!)
So, I made a little game. I told her she will be given a bunch of clues and if she guesses it properly, she gets her gift(s).
Time For A Birthday Gift Hunt:
I gave her the first gift along with the first clue which read, “Your second present is with a person who reads the story to you at bed-time”. Within minutes, she grabbed hold of her grandmother, who gave her well-deserved second present and next clue, “Your third present is with a person who packs your lunch-box for playgroup”. Jumping, she goes to her Mom. With the third gift in her hand, she listens to her next clue which is given by her Mom. “Your fourth present is with a person who carries you like a panda when you refuse to walk on your own”.
Her Dad. With all four gifts in her hand, the birthday gift hunt came to an end for her. But, with it, comes the beginning of an understanding of linked list for us.
What is Linked List in Data Structures?
Let me get you a formal definition and of course not-so-formal one where we unpack the jargon.
Formal Definition:
A linked list is a collection of multiple nodes where each node stores a reference to a data, as well as a reference to the next node of the list
A Not-So-Formal-Definition:
A linked list is a collection of multiple birthday presents where each present comes in two parts, one gift and a clue to get next gift.
 Oh yeah, our above birthday gift hunt example was nothing less than a linked list. So, let’s unpack the jargon.
Oh yeah, our above birthday gift hunt example was nothing less than a linked list. So, let’s unpack the jargon.
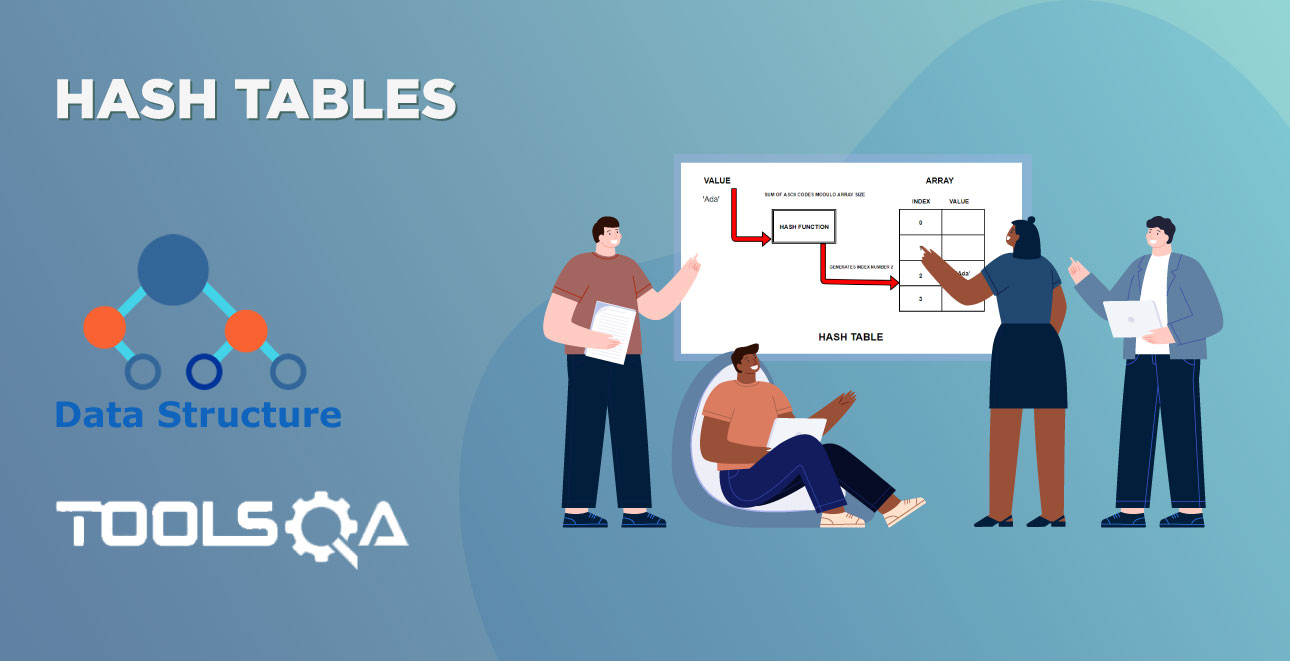
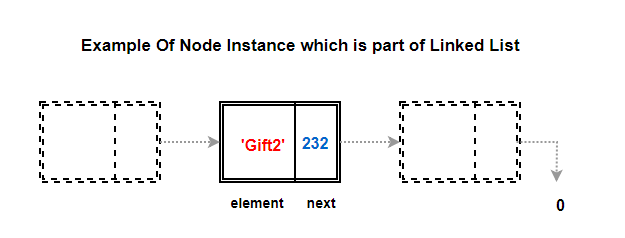
There’s something called a Node, which is the basic unit of the linked list.
You know what was a node in our above example?
Gift + Clue = Node
So, each node is made up of up parts:
-
Data part(gift)
-
Memory Address part of Next Node In the List(the clue)
Something like this.
It’s All About Head Node:
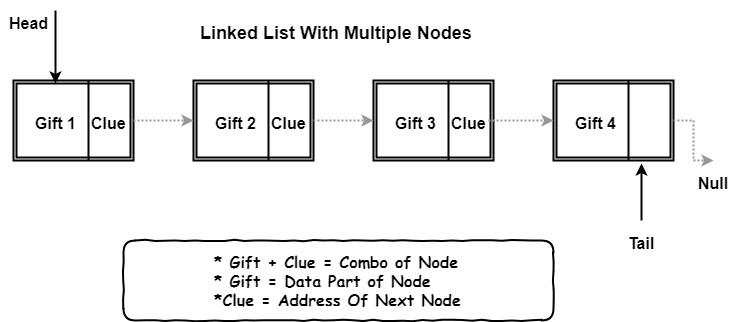
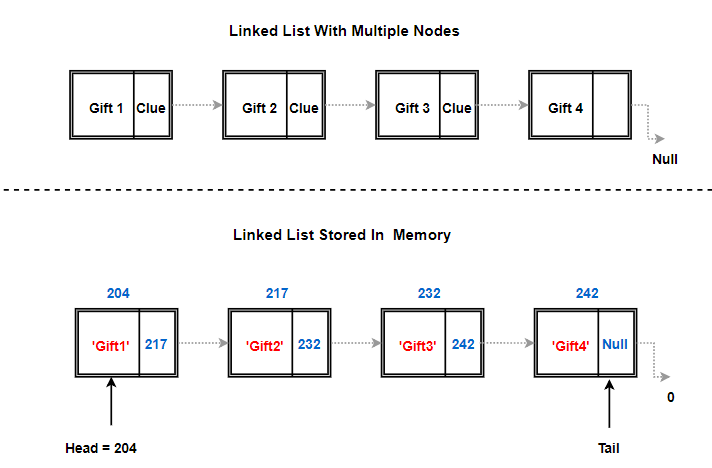
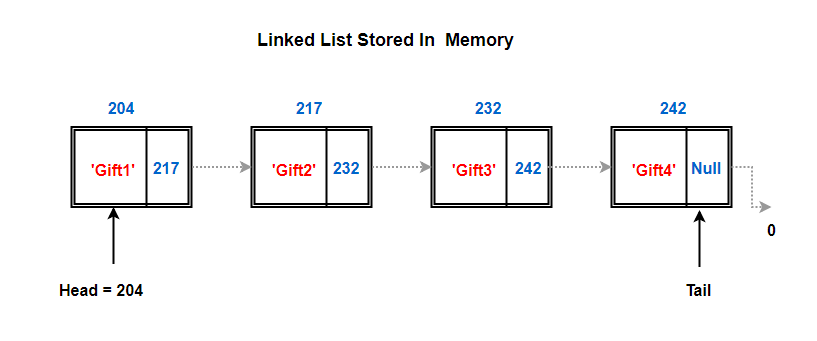
So, the first node of the list is called as the head node, represented by 204 (Memory address) in the above image. It is a really important node for two main reasons:
Our linked list knows only one memory address, the address where our head node is stored in the memory. In above example, head node is at memory address 204. This address of head node gives us complete access to the list (Remember for our gifts example, it all started with my clue. So, I was the head of the list in our gift hunt). Head node’s address field stores where the second node resides 217 in our case.
Traversing The Linked List:
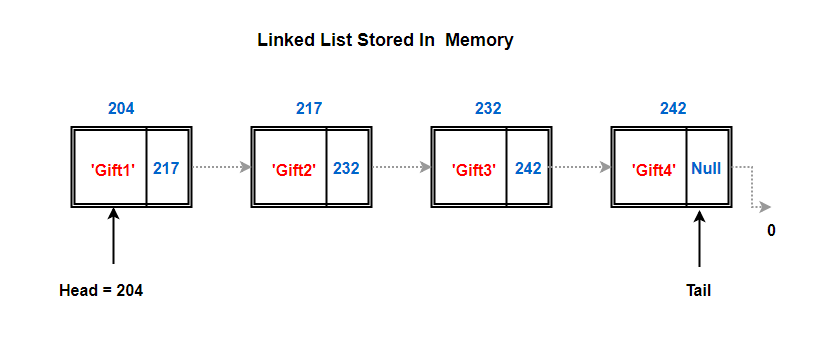 So, like we discussed before, we only know the address of our head node which resides in memory address 204. Off to the head node and ask it if it can tell us where the next node lies. It looks at the address part of its node and passes us the address of next node which is 217.
So, like we discussed before, we only know the address of our head node which resides in memory address 204. Off to the head node and ask it if it can tell us where the next node lies. It looks at the address part of its node and passes us the address of next node which is 217.
Again, we repeat the same steps, we go to node residing at address 217 and ask it to share the memory address of the next node.
This goes on till we hit a node which doesn’t have any address stored in the next field (null in above case).. Or it might link to what’s called a Terminator or Sentinel node. A sentinel node is really just a dummy node, a dummy object, that doesn’t contain any element value. This empty node can be used to identify the end condition of the Linked list.
This just means we’ve reached the end of the list. The last node in the list with no address is known as the tail node.
(N.B: This is still ordered data. But, just has a specific sequence of nodes with data and link to the next node)
Array Vs Linked List:
Bunch of nodes each storing data and address. Kind of work which our beloved array can do quite easily. Why bother studying linked list then?
Direct access Versus Sequential access:
Herein lies the major difference between a simple array and linked list. The way both these data structure are stored in the memory is very different.
Simple Array in Memory:
While storing elements of an array — whatever they are, integers, strings, references of objects — always imagine them stored in a contiguous area of memory.
Meaning the elements are next to each other.
 And thanks to this setup, no matter how large the array is, we can easily retrieve or jump to any position to see what’s stored there.
And thanks to this setup, no matter how large the array is, we can easily retrieve or jump to any position to see what’s stored there.
How? Did you guess it right? The Mighty indexes of arrays.
Direct/Constant Read-Write Access:
It is also fondly called as random access.
(I know the random word can mislead as we’re used to using this word for something we’ve no control over)
But, in data structure context, random access means we can get to any specific element directly without having to traverse backward and forwards through our entire collection.
The only operation which requires going through each and every single element in the array is a linear search. Except that, array supports direct access to the individual element. (Big O Complexity: O(1))
Sequential Access:
Like we discussed above, all linked list needs to know where our head node is stored in the memory. Head node can help us with addresses of other nodes easily.
So, nodes do not need to be located next to each other. They can be scattered anywhere in the memory.
Retrieving Element in Linked List:
 Now, let’s try to retrieve element ‘Gift 3’ from the linked list.
Now, let’s try to retrieve element ‘Gift 3’ from the linked list.
But, we’ve kinda hit a wall. We have no concept of index numbers in Linked List. And top of it, we don’t even know how to reach nodes without asking the head node to tell us where the second node resides in the memory.
So no direct/random access here. Consulting head node and following all the next field to find element ‘Gift 3’ is known as sequential access.
So, from array’s O(1) complexity to retrieve element to linked list O(n) complexity. Also, if needed array too can perform the sequential access. All we have to do it put a for loop, look at each element.
So, Array Gives Both Direct & Sequential Access, Why Study Linked List?
Because, it makes addition and removal of elements from collection much, much easier as compared to an array.
Inserting Or Deleting An Item In Array:
We know arrays are stored in contiguous space in memory, now to insert a new element in position 2 requires all elements to be shuffled around. Same goes if the element is deleted from any position. We need to maintain its meaningful index order. But reshuffling the items can be very demanding.
Big O Complexity For Operations On Array:
| Adding Element At | Add | Remove |
|---|---|---|
| Beginning | O(n) | O(n) |
| End | O(1) | O(1) |
| Middle | O(n) | O(n) |
How Linked List Solves This Insertion & Deletion Problem Like A Champ:
The below class Node — a nonpublic class — stores a node of linked list. Like we know, it is made up of two parts :
- data denoted as an element here
- address of next pointer denoted as next here
class Node:
# initialize node's fields
def init (self, element, next):
self.element = element # reference to gift
self. next = next # reference to next gift node
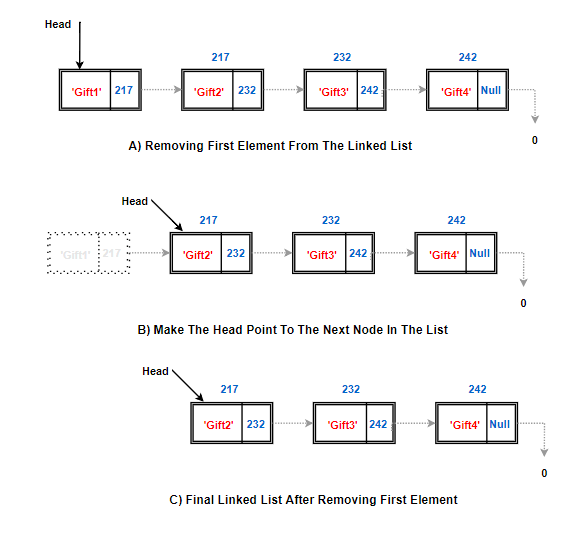
Removing First Node:
Back to our birthday gift example. Now instead of four gifts, I decided to give her only three gifts by excluding gift given by myself. Since I was the head node, before we get rid of it, we need to make next node as head node(Head node is the entry point which knows about the entire list. We need a head node no matter what)
Something like this:
Algorithm remove first(L):
if L.head is None then
Indicate an error: the list is empty.
L.head = L.head.next {make head point to next node (or None)}
L.size = L.size−1 {decrement the node count}
Explanation of Above Algorithm:
- Here, L stands for our linked list. First, we check whether our list has a head node. If not found, throw an error saying the list is empty
- But, if the head node is present, pick address of the next node from next field of the head node.
- Move the head pointer to the next node and decrement size of the linked list(from 4 gifts, we just have 3 gifts now).
Total Cost Of Operation: O(1)
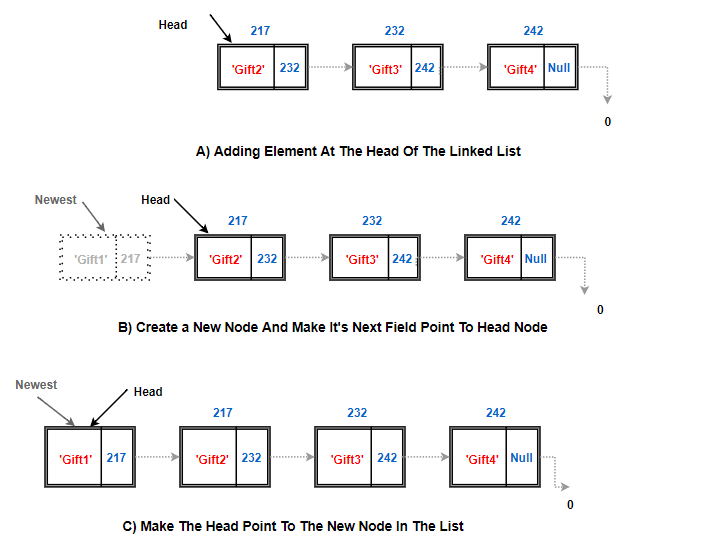
Adding A Node At The Beginning:
Let’s try to put my gift back as first present(head node)
Something like this:
Algorithm add first(L,e):
newest = Node(e) {create new node instance storing reference to element e}
newest.next = L.head {set new node's next to reference the old head node}
L.head = newest {set variable head to reference the new node}
L.size = L.size+1 {increment the node count}
Explanation of Above Algorithm:
- First, we create an instance of Node class. (Read all about class & object here)
- Now, since this newly created node will be the head node, make its address field point to the current head node.
- Then, move the head pointer and make it point to this newest node.
- This makes our newest node as head node and increment the size of the linked list.
Total Cost Of Operation: O(1)
Okay, one last one. I promise.
Adding A Node At The End:
Time to add one more present after Gift 4. The last node of the linked list is known as the tail node and usually has a tail reference/pointer like head node.
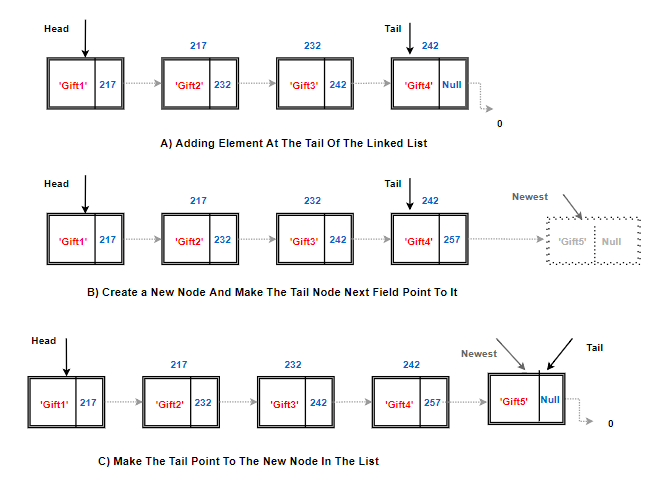
Algorithm add last(L,e):
newest = Node(e) {create new node instance storing reference to element e}
newest.next = None {set new node's next to reference the None object}
L.tail.next = newest {make old tail node point to new node}
L.tail = newest {set variable tail to reference the new node}
L.size = L.size+1 {increment the node count}
Explanation of Above Algorithm:
- First, we create an instance of Node class. (Read all about class & object here
- The last node or tail node next field has no value. Make it null.
- Make the next field of the current tail node to point to the newly created node.
- Move the tail pointer to the newly created node.
- Increment the size of the linked list.
Total Cost Of Operation: O(1)
Similarly, removing a node from the end will be O(1) operation. Everything still follows a sequence, no nodes need to be changed or shuffled around.
Now, imagine, even if we had a very large data, adding elements to a linked list always takes the same amount of time whether the list is small or large.
Something, which our array becomes inefficient at when the array is dealing with lots of data.
So, the array is extremely efficient at direct indexing(read/write) but bad at removing and adding elements.
Different Types Of Linked List:
The specific idea of a linked list which we discussed above so far is called a singly linked list.
Back to our birthday gift example, let’s say I don’t want to give her gift no 3, one which her mother gives her.
Delete Node From the Center:
We will have to follow below steps to delete a node from the center:
- To remove node no 3, all we’ve to do is make node 2 address field to point to node’s no 4 address.
- Start at node no 1. Follow each clue and reach Node no 3.
Simple. So, you reached Node 3. Time to delete it and make Node 2 next field point to Node 4.
But, Houston, we’ve got a problem.
How do we access Node 2?
Solution:
- A Not So Effective solution could be we store references of all past nodes while we follow clue and reach Node no 3.
- But, the best solution is to use a Doubly-linked list.
What is Doubly Linked List?
Works just like the single linked list but just with one extra superpower: Power to visit the past node.
How is it done?
Simply, by storing one additional piece of information for each node.
In the Singly linked list, we had a reference /address of just next node. In the doubly linked list, we have reference to next as well as previous node.
So, here the Node contains:
- data as element
- address of next node as next pointer
- address of the previous node as prev pointer
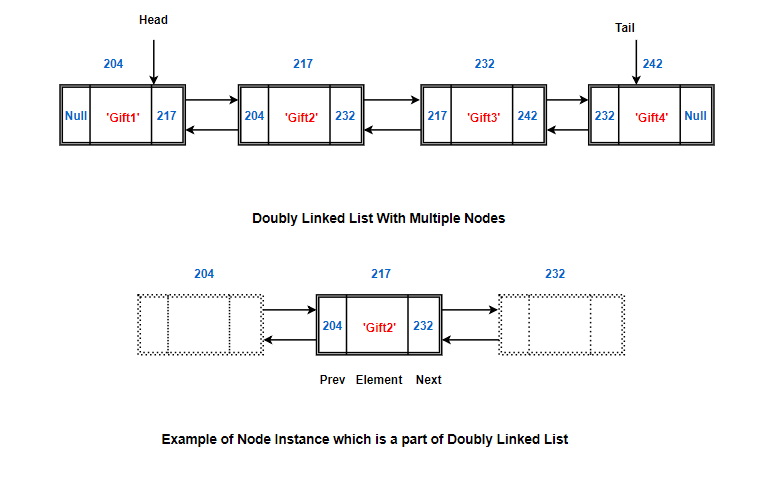
Nothing else is different. Just like the singly linked list, these nodes can be located anywhere in the memory. But each node has two references. A reference to the next node and a reference to the previous node.
Coming back to our removing node from center example, since doubly linked list allows us to go forward and backward, we can easily access node no 2 and make its next field point to Node 4.
So, thanks to the doubly linked list, along with adding and removing at head or tail node, we can easily insert/remove elements from center too.
First & Last Node Of Doubly Linked List:
So, just like the singly linked list, the last node might either be a null reference meaning we reached the end of the list. Or it might point to a terminator/sentinel node which explicitly indicates we’re at the end of the list.
Now, with the doubly linked list, we do the same thing with the previous link of head node too. So, it either stores null or points to the sentinel or terminator.
OR
We could make it a Circular Linked list.
What is a Circular Linked List?
Just like doubly or single linked list, just with one difference. Here, rather than these starting and finishing node(head & tail) pointing to a terminator, the tail node points back to the first node & head node references the final node.
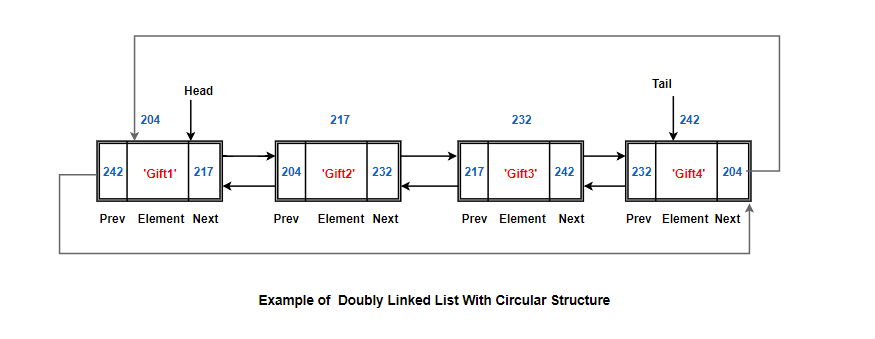 It’s not typical, but it can be useful for certain problems. But if we get to the end of the list and say next, we just start again at the beginning.
It’s not typical, but it can be useful for certain problems. But if we get to the end of the list and say next, we just start again at the beginning.
Basically, we go in a cycle/loop. If we follow the tail node next field, we will get the head node. Round robin scheduler can be implemented using circular linked list and the queue data structure.
Time Complexities Of Operations:
So, to summarize, let’s see the performance of various operations on the singly-linked list and doubly linked list.
There are several operations performed on the linked list and the names can sometimes be different in various environments and libraries. But normally the operations provided below cover most of them.
- Operations performed on the end of list performs well in the presence of tail pointer. In Constant Time i.e O(1).
- To check list is empty or check, look for head node. If not present, the list is empty.
- Like we discussed, adding an element before a node is not very efficient in Singly Linked List.
Big O Complexity For Operations On Singly Linked List:
| Singly Linked List | Operation Names | No Tail Pointer | With Tail Pointer |
|---|---|---|---|
| Add Element At The Front | PushFront(element) | O(1) | |
| Return Front Element | TopFront() | O(1) | |
| Remove Front Element | PopFront() | O(1) | |
| Add Element At The End | PushBack(element) | O(n) | O(1) |
| Return Last Element | TopBack() | O(n) | O(1) |
| Remove Last Element | PopBack() | O(n) | O(1) |
| Find A Element In The List | Find(element) | O(n) | |
| Delete A Element From The List | Erase(element) | O(n) | |
| Checking If The List Is Empty | Empty() | O(1) | |
| Adding A Element Before a Node | AddBefore(Node,element) | O(n) | |
| Adding A Element After A Node | AddAfter(Node,element) | O(1) |
But, We know how to make popping the element at the end and adding before cheap.
Yes, you guessed it right. We can do it by using doubly linked list. Thanks to the prev pointer, we can easily track the previous node.
So, to remove the last element, all we have to do it, go to the last node, check its prev field and move the tail pointer to the node address present in prev field.
Big O Complexity For Operations On Doubly Linked List:
| Singly Linked List | Operation Names | No Tail Pointer | With Tail Pointer |
|---|---|---|---|
| Add Element At The Front | PushFront(element) | O(1) | |
| Return Front Element | TopFront() | O(1) | |
| Remove Front Element | PopFront() | O(1) | |
| Add Element At The End | PushBack(element) | O(n) | O(1) |
| Return Last Element | TopBack() | O(n) | O(1) |
| Remove Last Element | PopBack() | O(1) | |
| Find A Element In The List | Find(element) | O(n) | |
| Delete A Element From The List | Erase(element) | O(n) | |
| Checking If The List Is Empty | Empty() | O(1) | |
| Adding A Element Before a Node | AddBefore(Node,element) | ||
| Adding A Element After A Node | AddAfter(Node,element) | O(1) |
Applications on Linked List:
Linked List is a very popular dynamic data structure. It is used to implement other data structures like stacks, trees, queues & graphs. So, all the applications of these data structures can be implemented with the linked list as well.
Other applications of Linked List are as follows:
- Undo Functionality
- Browser Cache
- Polynomial Addition
- Prioritized job queues